Передаточное отношение. передаточное отношение зубчатой передачи

Аналитическое определение передаточного отношения планетарного механизма

Рассмотрим порядок
получения формулы для расчета
передаточного отношения планетарного
механизма через известные числа зубьев
его колес на примере редуктора Джемса
(рис.1) или (рис.2,а).

Входным звеном в
этом механизме является солнечное
колесо 1, а выходным — водило Н.

Тогда искомым
является выражение
==?,
(2.1)

где обозначение
читается как “передаточное отношение
от 1-го колеса к водилу Н при неподвижном
3-м колесе”.

Для определения
передаточного отношения планетарного
механизма используется метод обращения
движения или метод остановки (“фиксации”)
водила.

Для реализации
этого метода всем звеньям механизма
сообщается дополнительное воображаемое
вращательное движение вокруг центральной
оси О₁О_н
с угловой скоростью (- _н).
Тогда получим новый — обращенный
механизм, который будет примечателен
тем, что его звено Н , бывшее ранее
водилом, станет неподвижным. Следовательно,
неподвижным станет и центр О₂,
т.е. обращенный механизм будет представлять
собой обычную зубчатую передачу с
неподвижными осями вращения колес. При
этом угловые скорости звеньев нового
обращенного механизма будут равны:

— солнечного колеса
1 — ₁
=₁-_н;

— корончатого
колеса 3 — ₃=0-_н=-_н;

— водила Н —
_н=_н-_н=0.

Таким образом,
при остановленном водиле ведомым звеном
становится корончатое колесо 3, и
передаточное отношение обращенного
механизма будет равно

=1-(2.2)

Следовательно,
искомое передаточное отношение
планетарного механизма
будет равно:

=1-(2.3)

где U(н)₁₃—
является передаточным отношением
обычной зубчатой передачи с неподвижными
осями, для которой по формуле Виллиса:

(2.4)

Тогда, подставляя
полученное значение, имеем для
планетарного механизма редуктора
Джемсa:

=1+.
(2.5)

Аналогично можно
вывести формулы для определения
передаточных отношений механизмов,
изображенных на рис.2.б, рис.3, а и б:

— для схемы на
рис.2.б:
=1+
; (2.6)

— для схемы на
рис.3.а:
;
(2.7)

— для схемы на
рис.3.б:
=
. (2.8)

При назначении
чисел зубьев колес планетарной передачинеобходимо
учитывать ряд требований и условий,
важнейшие из которых следующие.

1. Числа зубьев
Z₁,
Z₂…
должны быть целыми числами.

2. Сочетание чисел
зубьев колес должно обеспечивать
требуемое передаточное отношение U_пл
с допустимой
точностью ±3 % .

3. При отсутствии
специальных требований желательно
использовать в передаче нулевые колеса.
Это ограничение записывают в форме
отсутствия подреза зубьев: для колес
с внешними зубьями, нарезанными
стандартным инструментом, Z_i
≥ Z_min=17;
для колес с внутренними зубьями – Z_i
≥ Z_min=85.

4. Оси центральных
колес и водила Н планетарной передачи
должны лежать на одной прямой для
обеспечения движения точек по соосным
окружностям (условие
соосности ).

5. При расположении
сателлитов в одной плоскости, т. е. без
смещения в осевом направлении, соседние
сателлиты должны быть расположены так,
чтобы между окружностями вершин
обеспечивался гарантированный зазор

(условие
соседства)
:

(
Z₁+Z₂)sin
>Z₂+2,
(3.1)

где k
– число сателлитов.

6. Сборка нескольких
сателлитов должна осуществляться без
натягов так, чтобы зубья всех сателлитов
одновременно вошли во впадины солнечного
и корончатого колес:

,
(3.2)

где Z₁—
число зубьев центрального колеса,
k-число
сателлитов, р — число оборотов водила,
С_o-целое
число.

Рассмотрим порядок
синтеза планетарных механизмов,
представленных на рис. 2 и рис. 3.

3.4. Редуктор с двумя внутренними зацеплениями (рис. 3.Б)

Передаточное
отношение такого редуктора определяется
по формуле:

=
. (3.22)

Найдем зависимость
чисел зубьев Z₁
и Z₄
от

при условии обеспечения минимальных
радиальных размеров (минимальных чисел
зубьев).

Минимальное число
зубьев колес с внутренними зубьями
равно 85, а находящихся в зацеплении с
ними сателлитов равно 20.

Минимальная
разность чисел зубьев колес, находящихся
во внутреннем зацеплении, равно 8.
Обозначим разности чисел зубьев Z₁-Z₂=D
и

Z₄-Z₁=C.
Тогда Z₂=Z₁-D
и Z₃=Z₄-D.
После подстановки в (3.22) величин Z₂
и Z₃
получим:

=
, (3.23)

откуда

D
=
.

Здесь

– абсолютное значение передаточного
отношения.

Минимальное
передаточное отношение при Z₂=20
из (3.23) получается равным 26,5 , а максимальное
при D=8
равно 828.

Задаваясь разностью
С=Z₄-Z₁
в пределах от 1 до 4, можно при известном
передаточном отношении

найти D,
а затем и числа зубьев всех остальных
колес при Z₁=85:

Z₂=Z₁-D,

(3.24)

Z₃=Z₂+C=Z₁-D+C,

(3.25)

Z₄=Z₁+C.

(3.26)

Если при этом
получится Z₂<20,
то нужно увеличить С. Для предотвращения
многовариантных расчетов можно
воспользоваться графиком (рис.4),
построенным по результатам вычислений
при различных числах зубьев сателлитов
Z₂
с использованием (3.23) при передаточных
отношениях
=10…70.

Число зубьев
сателлита Z₂
и разность С должны быть выбраны по
возможности наименьшими, т.к. при этом,
во-первых, уменьшается масса колес
передачи и, во-вторых, появляется
возможность создания многосателлитной
передачи. Так, например, при U=30
целесообразно принять С=1 и с помощью
графика найти Z₂=22.
Тогда при Z₁=85
получим Z₃=22+1=23
и Z₄=85+1=86.
Передаточное отношения при таких числах
зубьев составит величину

=8622/8622-8523=-30.03
что на 0.1% отличается от заданного.

Рис.4. Выбор числа
зубьев Z₂
для различных
значений U_пл=10…70
и С=1…4

Количество
сателлитов можно определить из условия
соседства сателлитов второго ряда
колес передачи (рис.5), т.е. исходя из
чисел зубьев Z₃
и Z₄,
т.к. Z₄>Z₂.

В соответствии
со схемой зацепления, показанной на
рис.5, условие соседства сателлитов
примет вид:

где k-
число сателлитов.

Подставив сюда z3 из (3.25) и z4 из (3.26) и несколько преобразуя, получим:

sin
> –1, (3.28)

откуда
можно найти максимальное количество
сателлитов

k_max=
= . (3.29)

Рис .5. К определению
условия соседства сателлитов

На рис.6. представлены
результаты расчета максимального числа
сателлитов по формуле ( 3.29 ) для передач
с
=10…70
при разных значениях
с = 1…4. Как видно из анализа рис.6, с
увеличением передаточного отношения

максимально возможное число сателлитов
уменьшается и, например, для
=60
значение “C”
допускается только равным 1 и к_max= 3, а для С
≥ 2 и

≥ 40 возможен только один сателлит, и
водило превращается в кривошип.

Рис.6. Выбор
максимального числа сателлитов для
различных

значений U_пл=10…70
и С=1…4

Передаточное число — главная передача

Затем по зависимостям, установленным в теории автомобиля, определяют передаточные числа главной передачи и коробки передач, а также число передач.
 

Этими параметрами являются характеристика, рабочий объем и оборотность двигателя; передаточные числа главной передачи, коробки передач и демультипликатора.
 

Разные передаточные числа ступичных редукторов передних и задних колес в сочетании с передаточными числами главных передач переднего и заднего мостов обеспечивают одинаковые окружные скорости передних и задних колес, что необходимо для нормальной работы ходовой части тягача.
 

Повышение динамического фактора может быть достигнуто путем повышения крутящего момента двигателя или увеличения передаточного числа главной передачи. Улучшение динамичности грузовых автомобилей достигается за счет уменьшения их собственного веса, а легковых автомобилей — также и путем придания им обтекаемой формы.
 

Специально построенные газогенераторные автомобили ( заводского производства) отличаются некоторыми особенностями двигателя, увеличенным передаточным числом главной передачи и изменениями кузова и кабины в связи с размещением газогенераторной установки. Кроме того, на них устанавливаются специальные контрольные приборы и приспособления.
 

Мт — крутящий момент мотора, гк — передаточное число коробки передач, г — передаточное число главной передачи и — ij — кпд трансмиссии.
 

Тяговые качества грузовых автомобилей при постоянной работе с прицепами могут быть повышены за счет увеличения передаточного числа главной передачи при соответственном снижении их максимальной скорости.
 

Число оборотов привода спидометра, отнесенное к пути, пройденному автомобилем, обусловливается действительным радиусом качения шины, передаточным числом главной передачи автомобиля и передаточным числом привода вала спидометра.
 

Выбор числа оборотов того или иного подшипника зависит от средней эксплоатационной скорости автомобиля, от радиуса качения колес и от соответствующих передаточных чисел главной передачи и коробки передач.
 

Для того чтобы лучше приспособить грузовой автомобиль к заданным условиям эксплоатации, одно и то же шасси снабжается шинами либо стандартного, либо повышенного размера, с различным рисунком протектора, а передаточное число главной передачи соответственно подбирается. Самое короткобазное шасси данной модели используется не только для установки кузова-самосвала, предназначенного для перевозки компактных грузов, но применяется также и под тягач для седельного полуприцепа. Самое длиннобазное шасси снабжается обычно кузовом с решетчатыми бортами для перевозки емких грузов.
 

Исходными данными для предварительного выбора основных размеров и параметров зубчатых колес главных передач являются максимальное значение крутящего момента на ведущем зубчатом колесе главной передачи ( по двигателю или сцеплению ведущих колес), передаточное число главной передачи и0, а также ограничения по дорожному просвету.
 

Главная передача служит для передачи крутящего момента от карданного вала к полуосям ведущих колес под углом 90 и для повышения величины крутящего момента. Передаточное число главной передачи ( для легковых автомобилей 4 — 5, для грузовых 6 — 7) подбирается из расчета получения достаточной величины тягового усилия.
 

Автомобиль-самосвал МАЗ-205 изготовлен на базе автомобиля МАЗ-200 ( ЯАЗ-200) и отличается от него укороченной на 720 мм базой и укороченными вследствие этого карданными валами. Передаточное число главной передачи увеличено до 9 0 для улучшения тяговых качеств автомобиля при работе его в тяжелых дорожных условиях. Пневматический привод тормозов автомобиля несколько изменен, так как самосвал МАЗ-205 не предназначен для работы с прицепами.
 

Главная передача предназначена для увеличения крутящего момента, подводимого к ведущим колесам. Передаточное число главной передачи зависит в основном от мощности и быстроходности двигателя, назначения и общей массы автомобиля. Главные передачи могут быть с коническими, гипоидными или червячными шестернями.
 

Данные по автомобилю Москвич соответствуют передаточным числам коробки передач первой модели. Победа соответствуют передаточному числу главной передачи / 0 5 125 и передаточным числам коробки передач первой модели.
 

Червячная передача

Так как при определенных обстоятельствах вращательные движения выполняются под углом, то здесь требуется соответствующая система. В данном случае речь идет про червячную передачу. Как правило, главным элементом такой схемы выступает компонент цилиндрической формы. Кроме того, могут использоваться глобоидные механизмы, архимедов винт или эвольвентные изделия. В частности, это напрямую зависит от текущей поверхности, где расположилась резьба, а также от типа применяемой резьбы. В данном случае для вычисления передаточного отношения здесь используется число заходов всего червячного механизма. Как правило, этот показатель варьируется от единицы до четырех. Для того, чтобы высчитать необходимое число компонентов зацепления, здесь нужно использовать таблицу передаточных отношений для схемы червячного типа. В этой таблице собраны оптимальные данные, которые позволяют правильно подобрать правильное соединение для определенного изделия.

Необходимо принимать во внимание тот факт, что для червячной передачи присущи некоторые характерные недостатки. В частности, в процессе работы конструктивные элементы сильно нагреваются

В процессе работы может проявляться эффект проскальзывания. Существенный минус такой передачи в низком коэффициенте полезного действия. Червячные передачи не отличаются высокой надежностью. При работе могут появляться заедания, а также затормаживание. Из-за большого числа недостатков подобные механизмы в современном автомобилестроении применяются достаточно редко.

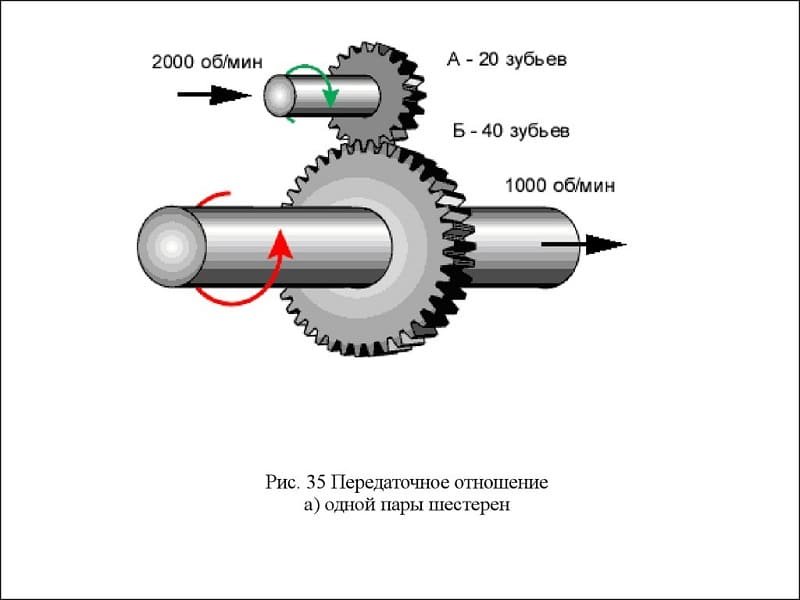
Передаточное отношение зубчатой передачи

Значение передаточного числа зубчатой передачи совпадает передаточным отношением. Величина угловой скорости и момента силы изменяется пропорционально диаметру, и соответственно количеству зубьев, но имеет обратное значение.

При схематическом изображении величины силы и перемещения шестерню и колесо можно представить в виде рычага с опорой в точке контакта зубьев и сторонами, равными диаметрам сопрягаемых деталей. При смещении на 1 зубец их крайние точки проходят одинаковое расстояние. Но угол поворота и крутящий момент на каждой детали разный.

Например, шестерня с 10 зубьями проворачивается на 36°. Одновременно с ней деталь с 30 зубцами смещается на 12°. Угловая скорость детали с меньшим диаметром значительно больше, в 3 раза. Одновременно и путь, который проходит точка на наружном диаметре имеет обратно пропорциональное отношение. На шестерне перемещение наружного диаметра меньше. Момент силы увеличивается обратно пропорционально соотношению перемещения.

Крутящий момент увеличивается вместе с радиусом детали. Он прямо пропорционален размеру плеча воздействия – длине воображаемого рычага.

Передаточное отношение показывает, насколько изменился момент силы при передаче его через зубчатое зацепление. Цифровое значение совпадает с переданным числом оборотов.

Передаточное отношение редуктора вычисляется по формуле:

где U₁₂ – передаточное отношение шестерни относительно колеса;

ω₁ и ω₂ – угловые скорости ведущего и ведомого элемента соединения;

Зубчатая передача имеет самый высокий КПД и наименьшую защиту от перегруза – ломается элемент приложения силы, приходится делать новую дорогостоящую деталь со сложной технологией изготовления.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Как рассчитать передаточное число

Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.

Расчет без учета сопротивления

В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.

u₁₂ = ± Z₂/Z₁ и u₂₁ = ± Z₁/Z₂,

Где u₁₂ – передаточное число шестерни и колеса;

Z₂ и Z₁ – соответственно количество зубьев ведомого колеса и ведущей шестерни.

Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».

При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.

Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.

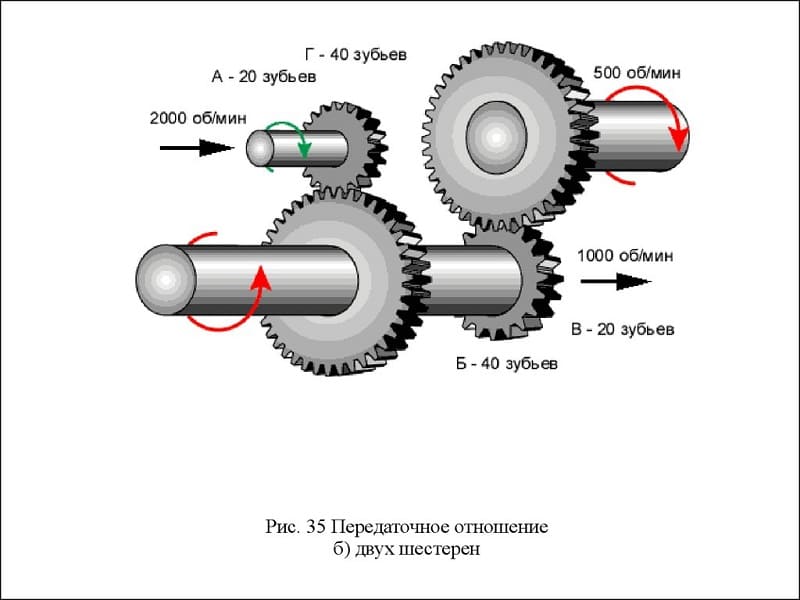
Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:

u₁₆ = u₁₂×u₂₃×u₄₅×u₅₆ = z₂/z₁×z₃/z₂×z₅/z₄×z₆/z₅ = z₃/z₁×z₆/z₄

Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.

КПД зубчатой передачи

Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:

• трение соприкасаемых поверхностей;
• изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
• потери на шпонках и шлицах;
• трение в подшипниках.

Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.

Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.

При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы  узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.

Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.

Основные геометрические параметры зубчатого колеса цилиндрической передачи

Рассмотрим
геометрические параметры зубчатого
колеса цилиндрической передачи в
плоскости, перпендикулярной оси его
вращения.

Каждый
зуб колеса имеет ось симметрии, проходящую
через ось вращения колеса О.
Угол между осями симметрии называется
угловым шагом
τ.
Число зубьев колеса z=2π/τ
(если τ
измеряется в радианах) или z=360º/
τ
(если τ
измеряется в угловых градусах). Внешняя
граница зуба очерчивается окружностью
выступов
радиусом r_a,
а внутренняя часть впадины – окружностью
впадин
радиусом r_f.

Геометрические
параметры зубчатого колеса

Окружность
радиусом r
делит зуб по высоте на головку
и ножку.
Расстояние между одноименными профилями
соседних зубьев по дуге этой окружности
(или между соседними осями симметрии
зубьев) называется окружным
шагом P.

Длина
окружности диаметром d=2
π r

L=Pz=
πd,

откуда

d=(P/π)×z.

Величину
P/π
= m
называют модулем.
На него введен ГОСТ 9563-60, в соответствии
с которым при расчетах геометрических
параметров зуб-чатых
колес его выбирают из стандартного ряда
в пределах m
= 0,05…100 мм.

Окружность,
по которой модуль m
является стандартной величиной,
называется делительной
окружностью
с диаметром d
= m×z
или радиусом r
= (m×z)/2.

Все
остальные геометрические параметры
зубчатого колеса в соответствии с ГОСТом
пропорциональны модулю m:

высота
головки зуба h_a
= m;

высота
ножки зуба h_f
= 1,25 m;

высота
зуба h
= h_a+h_f
= 2,25 m;

радиус
окружности выступов

радиус
окружности впадин

окружной
шаг P=π×m;

толщина
зуба по делительной окружности

ширина
впадин по делительной окружности

Ширину
колеса принимают в пределах в
= (10…30)m.
Межосевое расстояние двух зацепляющихся
колес нулевого зацепления

,

где
r₁
и r₂
– радиусы делительных окружностей
зацепляющих колес;z₁
и z₂
– число их зубьев.

В
зацепление друг с другом могут входить
только зубчатые колеса, имеющие одинаковый
модуль m
и окружной шаг P.

29

Крутящий момент редуктора

Крутящий момент на выходном валу – вращающий момент на выходном валу. Учитывается номинальная мощность , коэффициент безопасности , расчетная продолжительность эксплуатации (10 тысяч часов), КПД редуктора.

Номинальный крутящий момент – максимальный крутящий момент, обеспечивающий безопасную передачу. Его значение рассчитывается с учетом коэффициента безопасности – 1 и продолжительность эксплуатации – 10 тысяч часов.

Максимальный вращающий момент – предельный крутящий момент, выдерживаемый редуктором при постоянной или изменяющейся нагрузках, эксплуатации с частыми пусками/остановками. Данное значение можно трактовать как моментальную пиковую нагрузку в режиме работы оборудования.

Необходимый крутящий момент – крутящий момент, удовлетворяющим критериям заказчика. Его значение меньшее или равное номинальному крутящему моменту.

Расчетный крутящий момент – значение, необходимое для выбора редуктора. Расчетное значение вычисляется по следующей формуле:

Mc2 = Mr2 x Sf ≤ Mn2

где Mr2 – необходимый крутящий момент; Sf – сервис-фактор (эксплуатационный коэффициент); Mn2 – номинальный крутящий момент.

Достоинства и недостатки

Применение данной кинематической схемы наглядно показало наличие преимуществ.

К положительным моментам можно отнести:

• способность изменять направление передаваемого движения;
• широкая область применения;
• эффективно реализована передача, преобразование, увеличение мощности вращательного движения между осями передачи расположенными под углом друг к другу;
• достаточно широкий диапазон задания углов передачи крутящего момента от ведущего элемента к ведомому;
• широкая вариативность при компоновке разрабатываемых зубчатых и комбинированных систем;
• высокие нагрузочные характеристики (данные устройства способны передавать мощность величиной до 5000 кВт);
• эксплуатация и обслуживание не вызывает трудностей;
• удаётся получить высокий КПД.

К недостаткам специалисты причисляют:

• нагрузочная способность ниже, чем у цилиндрических конструкций (в среднем она на 20 процентов ниже);
• невысокая несущая способность (этот показатель ниже на 15 процентов);
• сложность и трудоёмкость в изготовлении колёс с заданными параметрами зубьев (количеством, величиной, углом наклона);
• повышенные требования к точности нарезания зубьев;
• возникновение повышенных осевых и изгибных нагрузок на все валы (особенно этот эффект наблюдается между валами, расположенными консольно);
• необходимость регулировки процесса передачи вращения;
• обладают большей массой, чем другие зубчатые передачи;
• высокие затраты на производство и обслуживание;
• возникают трудно разрешимые проблемы при проектировании и изготовлении систем с изменяемым передаточным числом;
• повышенная общая жёсткость конструкции.

Изменение передаточного отношения КПП: тюнинг коробки передач

Как известно, наилучшие динамические показатели достигаются в диапазоне оборотов максимального крутящего момента, а не мощности. Фактически, при нижнем и верхнем значении частоты вращения коленчатого вала крутящий момент двигателя меньше максимального.

Получается, чем больше обороты будут отличаться  от оборотов максимального крутящего момента, тем медленнее разгоняется автомобиль. В стандартных КПП передаточное отношение каждой ступени подобрано так, чтобы водителю было комфортно разгонять машину на низких передачах, после чего на повышенных можно поддерживать набранную скорость одновременно с экономией топлива.

Если же отбросить экономичность, тогда путем ряда доработок коробки можно улучшить динамику. Прежде всего, сужается диапазона частот, которые мотор развивает при езде на одной передаче. Фактически, передачи делаются более короткими, а также сближаются передаточные отношения передач, которые расположены рядом (сближенный ряд КПП).

На практике, мотор в этом случае быстро выходит на максимальные обороты на более низкой передаче, однако после переключения на ступень выше обороты не падают, например, 3500 об/мин. на 1800, а остаются на отметке около 2500. Фактически, после переключения «вверх» обороты все равно остаются в диапазоне максимального крутящего момента.

Для решения такой задачи можно использовать колеса с меньшим радиусом, а также требуется установить другую главную пару редуктора с измененным передаточным числом (например, 3.9 или 4.1 вместо 3.7). Начнем с использования «стоковых» деталей.

Как правило, если модель автомобиля выпускается с разными двигателями (например, моторы 1.2, 1.4 и 1.6 литра), тогда главную пару для КПП в паре с 1.6 литровым двигателем используют от той версии, мотор которой менее мощный (в данном случае  двигатель 1.2 или 1.4).  

В результате  после установки главной пары 3.9 или 4.1 передаточное число на 5-й передаче будет почти таким же, как и на 4-й при главной паре 3.7. Также дополнительно понизит общее передаточное число трансмиссии использование  шин меньшего радиуса. В результате  динамика автомобиля станет лучше, однако будет потеряна экономичность 5-й передачи.

На высоких скоростях двигатель будет на 5-й раскручиваться до максимальных оборотов, что может доставлять дискомфорт водителю и пассажирам. По этой причине ряд передаточных чисел КПП нужно подбирать с учетом конкретных задач и целей, учитывая мощность мотора, вес автомобиля, а также предпочтения водителя.

Если делать более серьезные доработки, тогда можно собрать коробку передач с измененным набором шестерен.  Естественно, это дорого, однако удается сблизить ряды на всех передачах, а не только 4 и 5.

Кстати, подбором передаточных чисел трансмиссии можно или улучшить разгонную динамику, или же повысить экономичность. При этом на практике во втором случае изменения в устройство КПП вносятся достаточно редко, так как штатно передаточное отношение зачастую подобрано достаточно удачно.

Также добавим, что стандартную 5-и ступенчатую коробку иногда переделывают в 6-и ступенчатую (особенно в паре с тюнингованным форсированным двигателем). Фактически, в КПП интегрируется комплект шестой передачи

Важно понимать, что  помимо высокой стоимости такой доработки снижается общая надежность такой коробки

Волновая передача

Ее работа основывается на принципе трансформации параметров движения благодаря волновому деформированию гибкого элемента механизма. По сути, такая передача является разновидностью планетарной передачи.

В состав волновой передачи входит жесткое колесо зубчатое, имеющее внутренние зубья, и вращающееся гибкое колесо с наружными зубьями. Оба колеса между собой входят в зацепление благодаря генератору волн, соединенному непосредственно с корпусом передачи.

За счет имеющихся конструктивных особенностей волновая передача наделена следующими достоинствами:

• Небольшие габариты и масса.
• Высокая кинематическая точность.
• Передаточное отношение передачи в одной ступени имеет большой показатель и вполне может достигать 300.
• Идеальная демпфирующая способность.
• Формирование в одной ступени большого передаточного отношения.

К недостаткам же относятся:

• Весьма сложная конструкция.
• Высокие потери мощности на трение и деформацию гибкого колеса (КПД составляет порядка 0,7-0,85).

Определение передаточного числа главной передачи.

Передаточ­ное число главной передачи находят исходя из максимальной ско­рости автомобиля на высшей передаче, заданной техническими условиями на проектируемый автомобиль.

Значение передаточного числа главной передачи определяют по формуле

Ur=3,6(wmaxrk)/VmaxUkUд

где vmax — максимальная скорость автомобиля, км/ч; wmах — мак­симальная угловая скорость коленчатого вала, рад/с; rk — радиус колеса, м; Uk — передаточное число коробки передач на высшей передаче; ид — передаточное число дополнительной коробки пе­редач на высшей передаче (ид = 1).

Полагают, что передаточные числа коробки передач на выс­шей передаче имеют следующие значения: ик= 1,0 — для прямой передачи и ик = 0,9…1,0 — для повышающей передачи легковых автомобилей; ик — 1,0 — для грузовых автомобилей с числом пере­дач не более шести; ик = 0,7…0,8 — для многоступенчатых коро­бок передач грузовых автомобилей.

Найденное расчетным путем передаточное число главной пе­редачи UТ должно иметь следующие значения: не более 5,0 — у легковых автомобилей; не более 7,0 — у грузовых автомобилей грузоподъемностью до 8 т; не более 8,0 — у грузовых автомобилей грузоподъемностью свыше 8 т.

Расчетное значение передаточного числа главной передачи не­обходимо сравнить с существующими передаточными числами главных передач автомобилей аналогичного типа и назначения. В том случае, если у новой модели автомобиля проектируется ве­дущий мост, то это значение передаточного числа уточняют с учетом числа зубьев шестерен главной передачи.

Определение передаточного числа первой передачи коробки передач. Определение передаточных чисел промежуточных ступеней коробки передач.

При опре­делении передаточных чисел коробки передач нужно помнить о том, что I передача предназначена для преодоления максималь­ного сопротивления дороги. Промежуточные передачи коробки пе­редач используются при разгоне автомобиля, преодолении повы­шенного сопротивления движению, работе автомобиля в услови­ях, не позволяющих двигаться с высокой скоростью (гололед, выбитая дорога, задержка впереди идущим транспортом и т.д.), а также при торможении двигателем на затяжных пологих спусках.

При расчете передаточных чисел сначала находят передаточ­ное число I передачи по заданному техническими условиями мак­симальному коэффициенту сопротивления дороги ψmах или мак­симальному динамическому фактору автомобиля по тяге Dmax на I передаче.

Это передаточное число определяют с помощью выражения, полученного из формулы для динамического фактора, пренебре­гая силой сопротивления воздуха, так как она незначительна при небольших скоростях движения:

u1=(Gaψmaxrk)/Mmaxηтрuгuд

где Ga — вес автомобиля с полной нагрузкой, Н; Mmax — макси­мальный крутящий момент двигателя, Н • м.

Полученное передаточное число I передачи коробки передач не гарантирует отсутствия буксования ведущих колес автомобиля. Чтобы не было буксования ведущих колес при движении на I пере­даче, необходимо выполнение следующего неравенства:

(Mmaxηтрuгuдu1)/ Gark≤Dсц=(mp2Ga2φx)/Ga

где Dсц — динамический фактор автомобиля по сцеплению; тР2 -= 1,20…1,35 — коэффициент изменения реакций на задних веду­щих колесах; Ga2 —- вес, приходящийся на задние колеса автомо­биля с полной нагрузкой, Н; фх= 0,6…0,8 — коэффициент сцеп­ления колес с дорогой.

Из этого соотношения определяют новое передаточное число I передачи, при котором буксования ведущих колес не будет:

u1=(mp2Ga2φxrk)/ Mmaxηтрuгuд

После проверки передаточного числа I передачи на отсутствие буксования ведущих колес автомобиля из двух найденных переда­точных чисел I передачи коробки передач для дальнейших расче­тов выбирают меньшее.

По этому значению передаточного числа I передачи и извест­ному значению передаточного числа высшей передачи определя­ют передаточные числа промежуточных передач.

Если высшая передача прямая (ип = 1), то для расчёта переда­точных чисел промежуточных передач используют следующее выражение:

Uk=

где п’ — число передач, не считая повышающую передачу и пере­дачу заднего хода; к — номер передачи.

Если высшая передача повышающая (ик < 1), то значение ее передаточного числа выбирают в соответствии с типом автомоби­ля, а остальные передаточные числа промежуточных передач рас­считывают с помощью приведенного выше выражения.

Передаточное число передачи заднего хода

Uзк=(1.2…..1,3)u1

Окончательное значение передаточного числа передачи задне­го хода определяют при компоновке коробки передач.

Рассчитанные передаточные числа коробки передач являются ориентировочными и при проектировании новой коробки пере­дач могут незначительно изменяться.

Форма зуба

Зацепления различаются по профилю и типу зубьев . По форме зуба различают эвольвентные, круговые и циклоидальные зацепления. Наиболее часто используемыми являются эвольвентные зацепления. Они имеют технологическое превосходство. Нарезка зубьев может производиться простым реечным инструментом. Эти зацепления характеризуются постоянным передаточным отношением, не зависящим от смещения межцентрового расстояния. Но при больших мощностях проявляются недостатки, связанные с небольшим пятном контакта в двух выпуклых поверхностях зубьев. Это может приводить к поверхностным разрушениям и выкрашиванию материала поверхностей.

В круговых зацеплениях выпуклые зубья шестерни сцепляются с вогнутыми колесами и пятно контакта значительно увеличивается. Недостатком этих передач является то, что появляется трение в колёсных парах. Виды зубчатых колёс:

Прямозубые колёсные пары имеют наибольшее распространение. Их легко проектировать, изготавливать и эксплуатировать .

Это интересно: Выпрямитель, схема диодного моста — рассказываем главное